Unpredictable Patterns #72: Monads, dyads and triads
Why you should care about connections, components, dimensionality, reducing problems, world models and how to visualize your challenges
Dear reader,
Thank you for the replies to last week’s musing on religion. There was a lot in what I heard from you that resonated - especially the observation that this is a modern problem in some sense, and that the modern instinct is to turn inward when facing anxiety. But the idea that there is, within us, a magical box of answers seems not just wrong, but dangerous - since what we are most likely to encounter is evolutionary remnants like tribal anger and destructiveness. There is a lot to that observation!
This week we explore relational thinking - and why we so often tend to the analytical monadism that suggests that things are primary to relationships and not the opposite.
Relational thinking
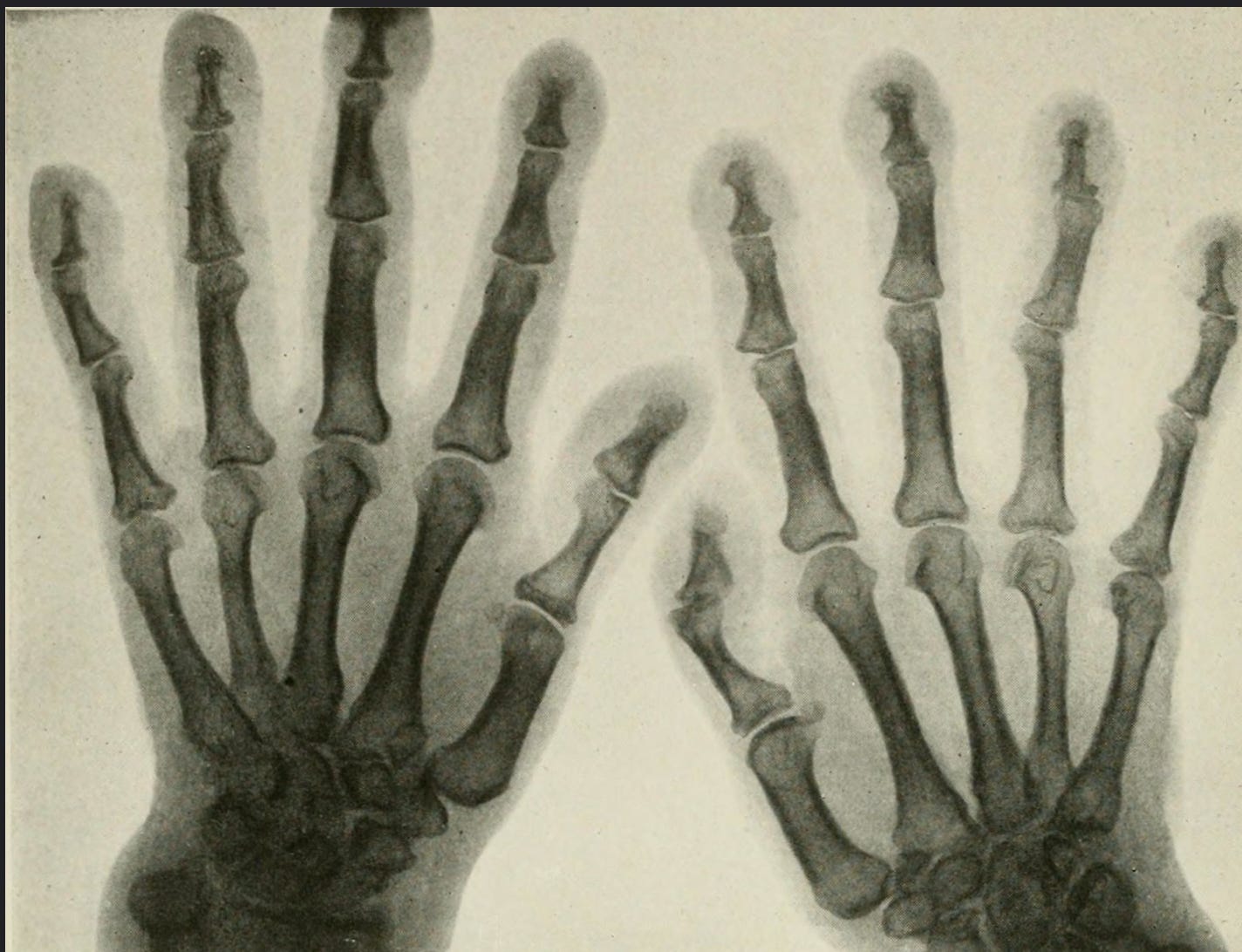
The way we see the world matters. Here is a very simple example: look at your hand. What do you see? Most people will, reluctantly, faced with such a trivial task, say ”five fingers” - and they will argue that this number - 5 - best captures the hand. But is it really that trivial? Here is Gregory Bateson’s on this question:
”You have probably been taught that you have five fingers. That is, on the whole, incorrect. It is the way language subdivides things into things. Probably the biological truth is that in the growth of this thing – in your embryology, which you scarcely remember – what was important was not five, but /four/ relations between pairs of fingers.”
Consider Bateson’s answer: he noted that what he saw was 4 relationships: between the thumb and the four fingers. Bateson’s perspective captures what is really important about the hand - the grasping - and so gives us a new way to see something we believe we already understand. It is about connections - relationships - rather than about components. (See more about Bateson if you are not yet familiar with his work here)
There is an interesting thread here to pull on: how we think about the basic parts of our world matters, and there are many different ways to divide the world up into parts, and these parts can be very different.
It is helpful here to think about this from a perspective provided by classical philosophy: we can thinking of our world as monadic, dyadic, triadic or tetradic. That is: we can assume that the basic building blocks are single, dual, three or four connected components.
Monadic thinking gets us the five fingers. We divide the world up into individual objects and look at these objects in themselves. This is helpful when learning about the world - look at a child that takes something apart to understand it - but it does not really tell us anything about function. The monadic view of life is essentially a list of all the smallest objects that we can divide up the world into.
Monadic models have come to dominate our thinking. We think about individuals, citizens, companies, countries and so one as individual components that can be understood outside any possible relationships. But as we adopt this perspective we also become blind to the functional nature of the things we look at. We see only the object, not its role in the a wider context - and sometimes that means that we do not understand the subject at all.
Monadic models suggest monadic evaluation and understanding. A monadic understanding of talent - to take on example - suggests that we can evaluate an individual performer without any concern for the partners they work with or the contexts they exist in. We make the individual the unit of analysis, and so seek solutions that are about the individual as well. This is particularly ironic, given that many companies are founded by more than one person, and this group actually is the best way to understand the company - not the individuals - and we often recognize this!
Monadic models can run deep and have profound implications, and challenging them can open up new vistas. Take the idea of artificial intelligence - and the concept of intelligence. Is that a single thing? In a single mind? An individual?
One of the early pioneers in AI, Marvin Minsky, suggested that the best model of the mind was a society of many agents, working together - and increasingly today we see adversarial networks do things that are quite amazing. Intelligence is not best understood as a monadic concept, but as something else - and so when we think about intelligence it is a relational concept - at least dyadic.
Another example is communication. Many companies will spend an inordinate amount of time on what they want to say and edit blogposts to death and beyond - but communication very clearly cannot be monadic - it has to have a receiver! But how many times have you seen a discussion about comms from a company start with what you want the receiver to say in response to your statement? An alternative way to communicate would be to start with writing what you want the recipient to say in response to your statement, and then reconstruct the statement from there.
This leads us to the second model - the dyadic. Dyadic models suggest that there are no single components in our world, but everything needs to be understood in pairs. This sounds fluffy, and even a bit new agey, but in reality this is probably the best way to capture what the world is actually like. Nature exists in a set of forces that all interact with each-other, quantum physics suggests, in some interpretations, that the observer has a key role to play and we are - to quote the existentialists - only individuals in relationship with the Other.
Our self is strewn in the gaze of others, as Heidegger liked to note.
Dyadic models suggest that we look at the world as a set of pairs. The pairs can vary, but a dyadic perspective never allows for any single thing to be the key to understanding a model. Talent is about the individual and their team, perhaps divided up into meaningful dyads - suggesting that the health of a team can be assessed on the basis of how many functional dyads the team can create: the more the better. Communication always starts from the recipient, and we look to the dialogue as a model over the monologue.
We do have some dyadic instincts in the way that we view the world. We tend to see both cause and effect, for example. This relationship is so strong that Kant suggested that it was a category of perception necessarily imposed on us (in response to Hume’s disinterested observation that there was no causality to be observed anywhere - a deeply monadic observation where your concepts had to be justified from the monads Hume picked). Cause and effect are dyads that sequentially make up a large part of how we perceive reality, yet we often isolate them and think we can look at one cause and its effect, rather than the network of different causes.
This line of thinking is interesting too, since it underpins so much of our everyday models. Take the question of technological development and social change. Here we are stuck in dyadic thinking that goes just one way: we tend to think that technological development leads to social change. This single causal relationship is usually taken for granted, but it leaves a huge hole in the model of the world we work with: where did technological development come from? What is the cause of technological development?
The inability to answer that question - or the lack of interest - leads to a perspective where we end up thinking that we need to stop, change or slow technological development to sort social change. That is simplistic at best - and here we could do even better to use a triadic model: we could argue that both technological and social change actually are caused by an increase in complexity in our environment, and then our discussion would have to be broader - to just take one example.
Triadic thinking is far less usual in our everyday models of the world, but it is surprisingly persistent in more complex models of the world.
Semiotician and thinker CS Pierce famously noted that he had a tendency to think in threes - exemplified by his semiotics, where the sign is a part of a triadic relationship, and we see echoes in this for every person who speaks in threes in a presentation or speech. Triads are useful to illustrate more complex phenomena in the world.
Triads also are more common in mystic thinking - the holy trinity is the most obvious example, but there are others as well, across many religions. When we think in triads we need to imagine a world that is constituted by relationships between three different components.
Such world models are hard to work with, and we tend to collapse back into dyadic or monadic models when we try - but it can be helpful to think about how persistent these triadic models can be. The atom consists of neutrons, electrons and protons - and this is what makes up basic matter in our more coarse grained physical models.
To be able to imagine a third way is often the key to break out of a dilemma (or at least turn it into a trilemma) - and escape the horrible cage of the ”tertium non datur” (there is no third) set up for us within Western logic. This is the synthesis of the thesis and the anti-thesis, the melding together of opposites.
Lastly, then, we meet the tetrad models - where the world is made up of four different things: earth, wind, fire and water are the four elements, and we suddenly have a very different and much more complex model of the world that brings us back to the ancient pre-socratics.
The tetrad completes our different models, and as it does so it also opens up others. The monad, dyad, triad and tetrad together give us the ten - the perfect number (as 1+2+3+4=10), and this is why the pythagoreans worshiped it in their prayers:
”Bless us, divine number, thou who generated gods and men! O holy, holy Tetractys, thou that containest the root and source of the eternally flowing creation! For the divine number begins with the profound, pure unity until it comes to the holy four; then it begets the mother of all, the all-comprising, all-bounding, the first-born, the never-swerving, the never-tiring holy ten, the keyholder of all.”
Anyone who manages to move between monadic, dyadic, triadic and tetradic world models will have a natural advantage over those of us who are stuck in the monadic images of the universe.
Dimensionality
The question of world models is really a specific case of a much harder question - and that is the question of the dimensionality of problems. As pointed out by David Krakauer in a recent podcast from the Santa Fe institute, we really like problems to be two-dimensional, and consist of, say time and change in some quantity over time, even if just to be able to draw it in a diagram. But, he noted, problems may not be described best in two dimensions, and we should break free from this visualization trap - or at least be aware of it.
The dimensionality of a problem is essentially the number of different factors that meaningfully impact the way the problem evolves - to simplify - and in many cases it will not be enough to stick with just two different dimensions. To look at a challenge and list the dimensions that it consist of is helpful in two ways: the first is that we can get a ballpark understanding of the problem’s complexity - higher dimensionality implies higher complexity to some degree - and the second is that it allows us to figure out if the dimensions can be broken out and studied separately or if they are wickedly connected in ways that allow for no separation or reduction.
We may also want to practice the skill of thinking in higher dimensions than 2, because that will help us understand the field we are studying much better. An interesting example of this that is oft-cited, is how master chess players see the board. They see fewer possible moves, and this seems to suggest that expertise is about ignoring all the moves that are irrelevant. One interpretation of this has been that they simply focus on the meaningful moves, but another - equally plausible - interpretation is that they see higher-dimensional objects. They see not just monads, but dyads, triads, tetrads and from these complex relationships they see not fewer moves, but just the moves that are possible within the higher dimension understanding if the game. This ”gestalt”-interpretation of expertise skill suggests that it could be connected to moving away from the simplistic monad understanding of a problem, away from the amateur chess players focus on the individual pieces on the board to the structures - relationships - on the board.
What would an example look like?
Well, let’s look at competition policy. The low-dimensional understanding of competition policy suggests that we look at two dimensional models: consumer benefit and company behavior, or innovation and company behavior. A specific behavior is interesting to a competition agency if it violates a single criterion in some way: does it impact consumer behavior, or the overall pace of innovation? This is the model of competition policy that is encapsulated in law - law usually needs to reduce dimensionality to get to manageable decision making guides - but the real problem of competition policy also contains entirely different dimensions.
Two of the most obvious ones are size and success.
A large and successful company will have a harder time with competition issues than a small and failing company - but this is not captured will in the simpler models. And if we also add time and note that persistently large and successful companies are under even more competition policy scrutiny - no matter the outcomes for consumers or innovation - we see that the solution space for competition policy concerns is actually quite narrow for a persistently large and successful company: they end up in the curse of bigness (to steal and slightly change a term from Justice Brandeis) where the only test for the adequacy of a political intervention is if it reduces a company’s size and success.
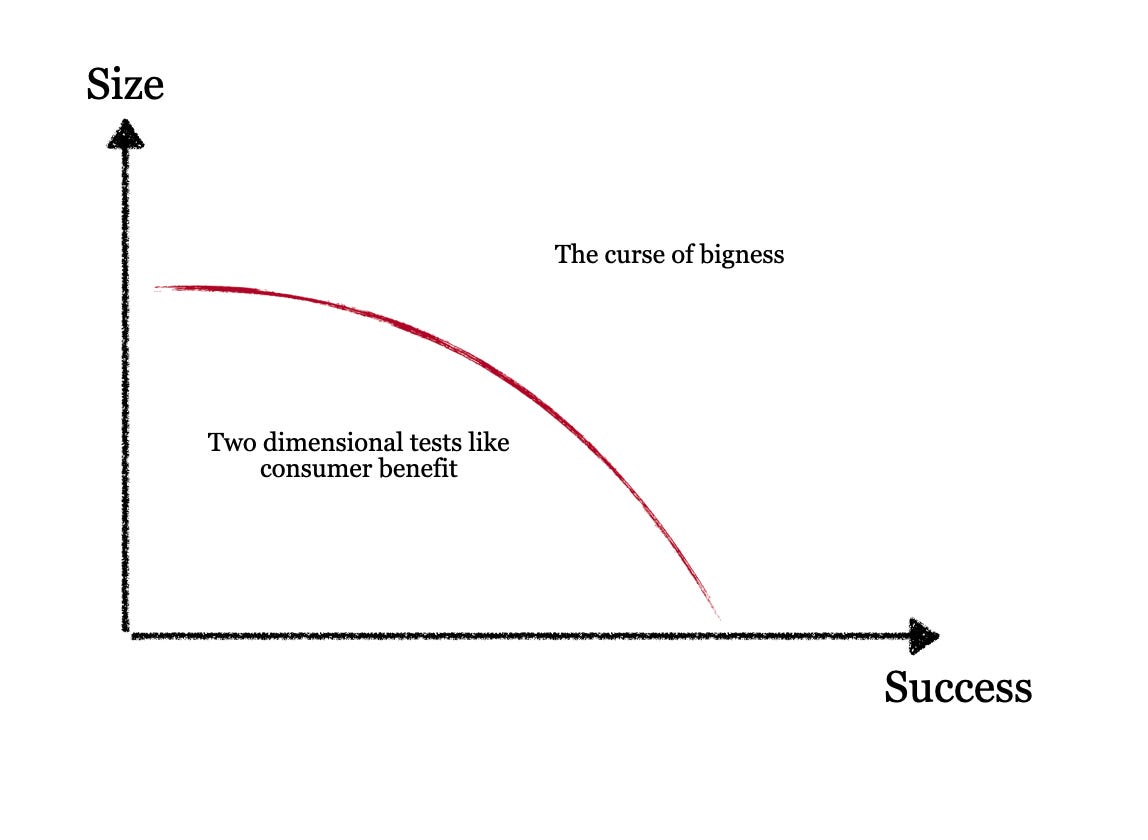
And we can go further and try to understand the dimensions of success and size as well - they are likely to be even more complex.
The overall conclusion is that even if the two-dimensional analysis seems positive, and a company should be able to prevail in court - the higher dimensions of the problem suggest that this will just lead to legislation and a reigning in through other means. The competition problem for the tech sector is not a two-dimensional problem, and if anything it seems to add more dimensions - like geopolitics - over time, and so is becoming increasingly hard to reduce to lower dimensions.
And there is another problem here as well - when the dimensionality of a problem increases, the data becomes sparse. The reason is self-evident: the possible data sets grow very quickly with the dimensionality of the problem. This curse of dimensionality means that when we face a growing number of dimensions in a problem the data we have is likely to be sparse, and then it is hard to learn fast enough - with or without tools - for that particular problem.
Reducing dimensionality, then, becomes imperative - but naturally also very hard. Yet this is what we always have to do to understand the world - that is how we end up with two-dimensional problems! An important insight here - as Krakauer notes - is that we tend to reduce dimensionality through visualization. This means that we need to find new ways of visualizing our problems in higher dimensions. This is hard, but we can certainly do better than the simple chart - so exploring different visualization models is actually not just a nice-to-have, but a need-to-have for us to really build new models.
Bateson’s genius lay in - among other things - the way that he showed the dyadic model of the hand by simply touching the thumb with the other fingers: we see it and so we understand it. The fingers - monads - are set in motion and relation to each-other, and we see the dyads.
There is a pessimistic hypothesis here: that we cannot solve problems that we cannot visualize well. We don’t need to go so far, but we can note that if we can visualize a problem with higher dimensionality well, we have a better chance to solving and understanding it better.
So what?
We know full well that our models of the world matter. But changing these models is hard, and abandoning them impossible - indeed, often even unwise. So finding new ways that we can build them - new construction tools - is a key thing for us. The idea of dimensions and n-yads is simple a building tool for world models, and a classification method for the naive models we deploy. There is a lot you can do here if you are so inclined.
First, check your existing models for dimensionality and basic components. Are they monadic? Dyadic? How many dimensions do you allow for?
Second, try consistently to apply dyadic and triadic models of the world across your work. What would it mean to understand your work relationally?
Third, check hard problems for dimensionality - what have you reduced out and why?
Fourth, visualize in more ways than one. Draw your problem in at least three different ways - and then ask others how they would draw it. Tease out the dimensionality you assume as an organization.
All of this is easy to do, but presents a small initial threshold: no one wants to be the person who says ”but what about dyadic models” in a meeting - because it sounds theoretical and perhaps abstract. So it is worthwhile developing other questions here, questions that you are comfortable with asking. Here are a few suggestions:
”What does this relate to? Who is the audience or recipient?”
”What are the relationships here that we need to understand?”
”How would we visualize this?”
”Are there other possible causes for our problem here?”
You will have other ideas - and surely better ones. The right questions, however, will allow you to overcome that initial threshold - and might just present small revelations, just like Bateson’s question did for me.
Thanks for reading,
Nicklas




Thank you for writing this! Such a great piece to point peeps to in the future.